【GPyOpt】Python x ベイズ最適化の基本をマスターしよう

　この記事ではPythonで最適化を行うための有力な手法であるベイズ最適化を紹介し、ベイズ最適化のライブラリとして汎用性の高いGPyOptについて解説します。

連続最適化

　最適化問題という分野はかなり幅広く1つの記事では網羅できません。例えば、最適化にも連続最適化と離散最適化があり、それぞれの中でも様々な最適化手法がありますが。ここでは連続最適化に焦点を当てます。連続最適化とは言葉の通り、最適化したい関数(目的関数といいます)が連続的な数値を取る場合の最適化です。

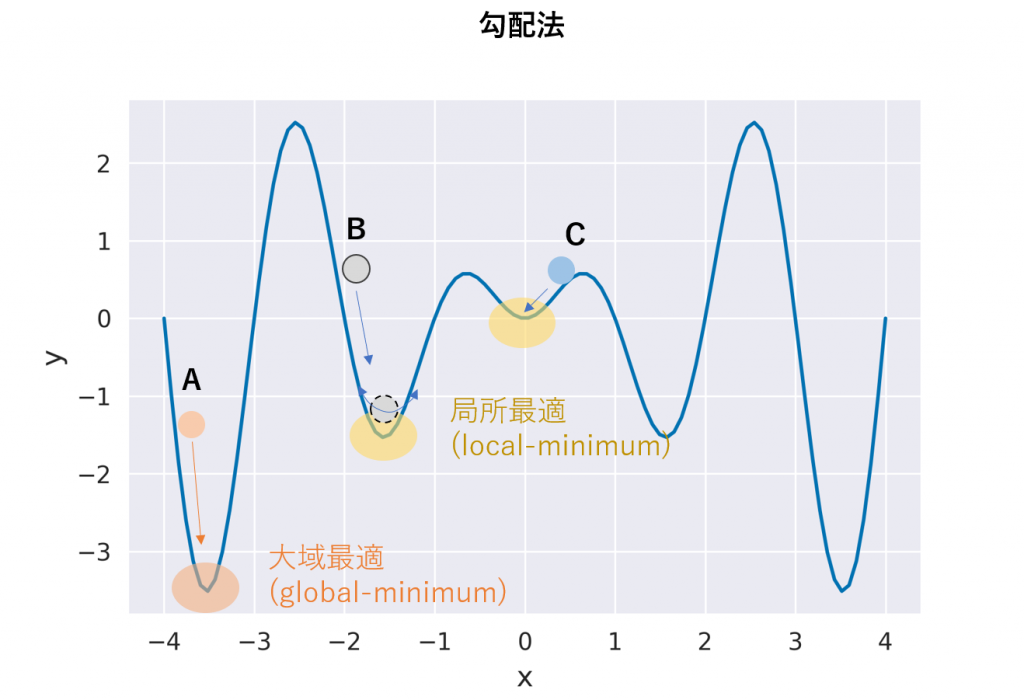
　連続最適化のための手法としては、最適化したい対象の関数の形が解析的にわかっていて、微分可能な場合は勾配法やNewton法といった目的関数の勾配の情報をうまく利用した手法があります。勾配法では勾配情報を使って目的関数の極小値を探すアルゴリズムですが、目的関数が多峰性を持つ場合には局所最適に落ち込むことがしばしばあります。

　局所最適とは下図のように、極小値ではあるが、全体を見たときに最小値ではないポイントの事です。この例ではA, B, Cの３つの異なる初期値から出発した場合にAから出発したものだけが大域最適に到達できます。勾配法は坂を下っていく手法のため、原理的に局所解に陥りやすい手法です。

ベイズ最適化

　これに対してベイズ最適化は比較的局所解に陥りにくく、効率の良い最適化手法です。ベイズ最適化は名前の通りベイズ統計に基づいた最適化手法になります。つまり、ベイズの定理に基づいて事後分布という分布を考えます。分布を考えると何が良いかというと、分布の平均値だけでなく、データに基づいた信用区間も考慮することができる点です。言葉で説明するより、図を見た方が早いと思われますので、下図を見てください。

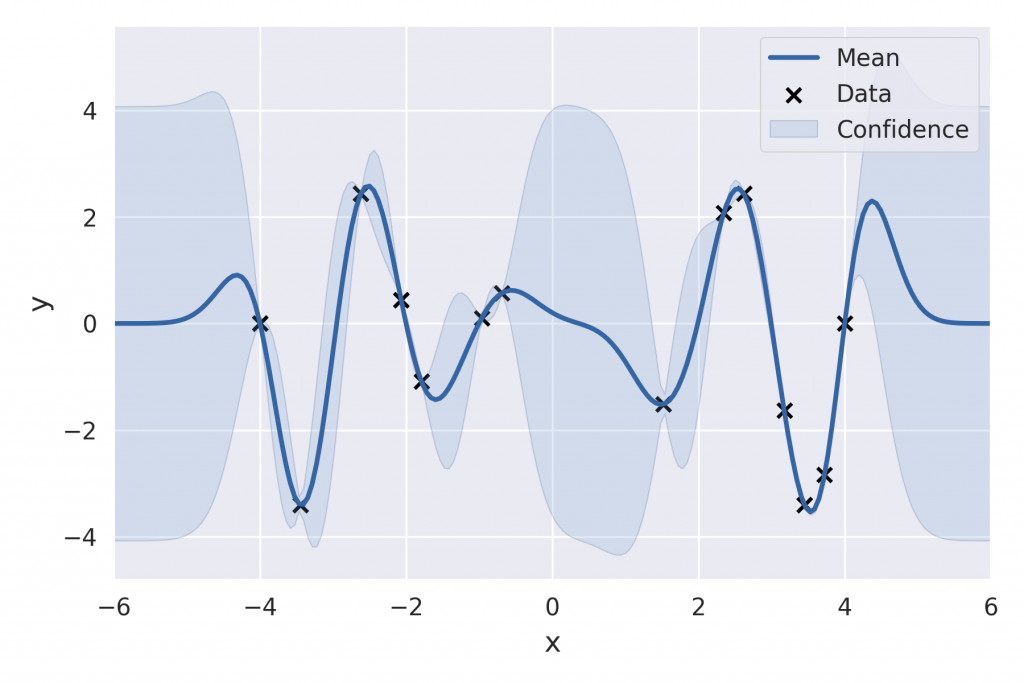
meanと書かれている実線が分布の平均値、そして、青で塗りつぶしている領域が信用区間です。この例では、xが 0 ~ 2の間にデータが無いので、不確定性が大きい領域だということが分かります。このようにベイズ最適化では目的関数の分布を考えながら、次の解の候補を探すため、局所解に陥りにくく、最適化効率も良いです。

【GPyOpt】Pythonのベイズ最適化ライブラリ

　Pythonではベイズ最適化を簡単に行えるGPyOptというライブラリがあります。以下ではこのGPyOptの使い方を解説します。

インストール & import

まず、GPyOptのインストールですが、pipで次のようにインストールします。

pip install gpyopt

ライブラリのimportは次の通りです。

import GPyOpt

基本の使い方

GPyOptの使い方ですが、大まかな流れとしては、次のような３ステップです。

1. 最適化する関数を作成
2. 最適化する変数の設定
3. 最適化する

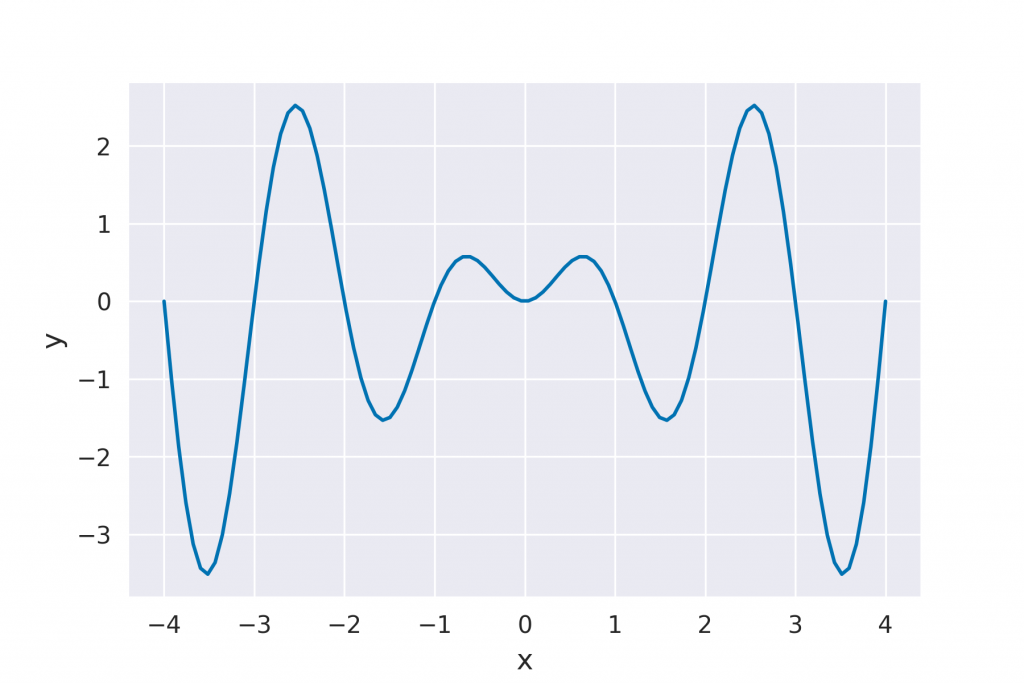
ここでは次の関数を例に説明します。

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

sns.set_style('darkgrid')

"""
 generate dataset & plot
"""
func = lambda x :  x * np.sin(np.pi  *x)
x = np.linspace(-4, 4, 100)
y = func(x)
plt.plot(x, y)

①最適化する関数を作成

まず、１の最適化する関数を作成するステップですが、今回は次の関数です。

func = lambda x :  x * np.sin(np.pi  *x)

　目的関数が解析的に分かっておらず、数値シミュレーションなどとベイズ最適化を組み合わせる場合はTipsで解説します。

②最適化する変数の設定

　ここでは、最適化する変数を設定します。変数の設定とは連続変数なのか離散変数なのかや、また変数の値域などの設定を行うことです。ここではｘという連続変数を(-4, 4)の範囲で最適化することを想定し、次のように設定します。変数の設定ですが、リストの中に辞書で記入します。

bounds = [{'name': 'x', 'type': 'continuous', 'domain': (-4, 4)}]

③最適化する

　最後に最適化する関数と変数の設定を最適化オブジェクトに渡して、最適化します。その際に、max_iterという最大繰り返し回数を指定する必要があります。ここでは最大10回の繰り返しを設定しています。実際には10回繰り返す前に５回ランダムなサンプリングが行われます。

my_bopt = GPyOpt.methods.BayesianOptimization(f=func, domain=bounds)
my_bopt.run_optimization(max_iter=10)

最適化が完了したら、得られたその時点で得られた最適解はx_optに入っています。

print(my_bopt.x_opt)

ここでは出力値は次のようになりました。上のグラフを見て分かる通り、最適な解が得られている事が分かります。

[-3.51664712]

獲得関数の表示

　ガウス過程回帰に基づいた現在の目的関数の事後分布と次にサンプリングするポイントを示すには次の関数を用います。赤の縦線が引かれているポイントが次にサンプリングを行うポイントです。

my_bopt.plot_acquisition()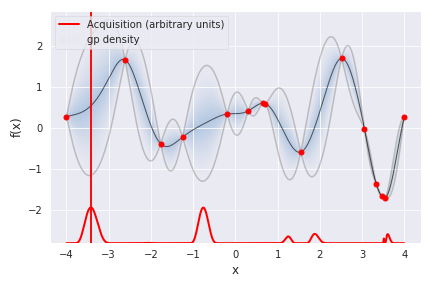

収束状況の確認

　試行回数ごとの収束状況を確認するには次の関数を用います。ここでは最初の３回程度でほぼ最適解が得られている事がわかります。これは最初の５回のランダムな試行にも依存するため、やるたびに結果が異なります。

my_bopt.plot_convergence()

ベイズ最適化 vs ランダムサーチ

　ベイズ最適化がどれくらい効率が良いかを調べてみます。ここでは、上の最適化問題を使って、他の最適化手法(ランダムサーチ)とベイズ最適化との比較を行います。ランダムサーチを行うライブラリは無かったため、次の自作の関数を用いました。

def random_search(x_arr, expr, max_iter=30):
    """
    x_arr    param: Numpy Array for random choice
    expr     param: objective function
    max_iter param: max iteration
    """
    out_best = None
    x_choices = np.random.choice(x_arr, max_iter, replace=False)
    x_list = []
    out_list = []
    convergence = []
    for i, x in enumerate(x_choices):
        out = expr(x)
        if i == 0:
            out_best = out
        else:
            if out < out_best:
                out_best = out
        x_list.append(x)
        out_list.append(out)
        convergence.append(out_best)
    return out_best, x_list, out_list, convergence

　ランダムサーチもベイズ最適化も確率的に振舞うため、複数回最適化を行った平均値を計算し、統計的なパフォーマンスを調べています。ランダムサーチに関しては40回、ベイズ最適化は10回の統計平均を取っています。結果を次に示します。

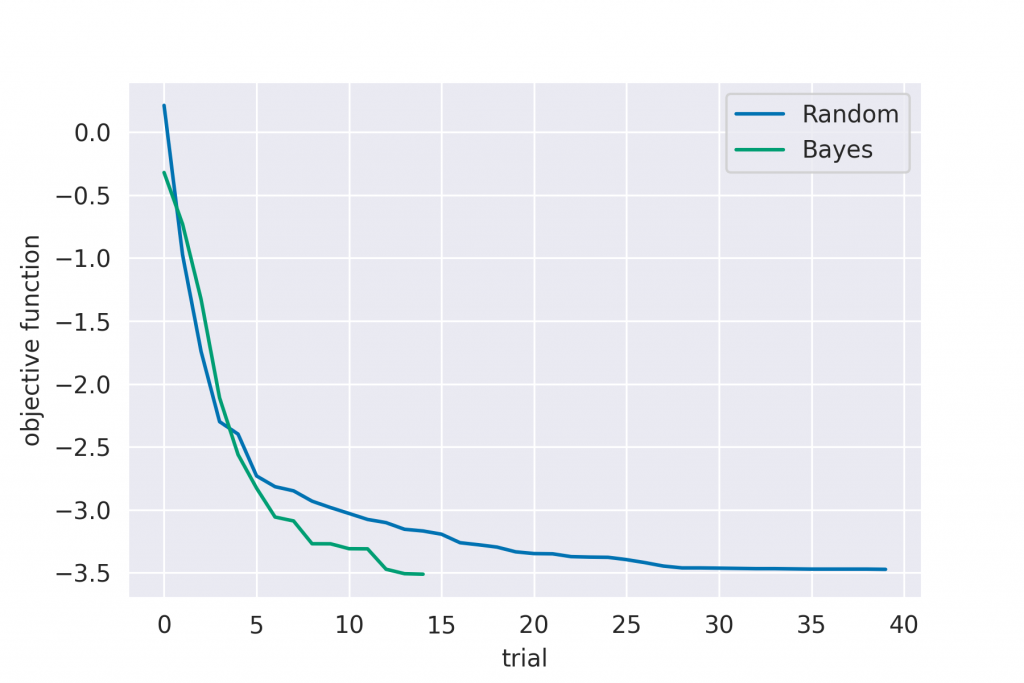
　これを見ると分かりますが、まずランダムサーチでは最適解に到達するまでに平均的には30回以上かかる事が分かります。一方でベイズ最適化では１２, １３回程度で最適解に到達しています。この為、ベイズ最適化はランダムサーチと比較すると2, 3倍のパフォーマンスが出る事が分かります。この例では１次元ですが、２次元以上では解の組み合わせがもっと増える為、ランダムサーチとの差はより大きくなると考えられます。

コード全体

ベイズ最適化のコード全体は次の通りです。

import numpy as np
import matplotlib.pyplot as plt
import GPyOpt

func = lambda x :  x * np.sin(np.pi  *x)
bounds = [{'name': 'x', 'type': 'continuous', 'domain': (-4, 4)}]
my_bopt = bopt.methods.BayesianOptimization(f=func, domain=bounds)
my_bopt.run_optimization(max_iter=10)

#
# 最適化後
#
my_bopt.plot_acquisition()
my_bopt.plot_convergence()
print(my_bopt.x_opt)

Tips: 数値シミュレーションとベイズ最適化の組み合わせ

　数値シミュレーションとベイズ最適化を組み合わせる例を紹介します。ここでは例として、流体力学の最適化問題として、圧力損失を最小化するための流路設計の例を考えてみます。以下にコードの例を示します。

#
# 関数の中でシミュレーションを行い、圧力を返す関数
#
def run_bayes(*args):
    # 最適化する変数はdomainで定義した順番で関数の引数に渡される為、
    # *argsで受けて、順に格納
    x1 = args[0]
    x2 = args[1]
    # シミュレーションを実行し、圧力を返す
    sim = CFD(x1, x2)
    sim.init()
    sim.run()
    pressure = sim.get_pressure()
    return pressure
#
# 最適化変数を定義
#
bounds = [{"name": "x1", "type": "continuous", "domain": (-4, 4))},
          {"name": "x2", "type": "continuous", "domain": (-4, 4))},
          ]
#
# 最適化を実行
#
my_opt = GPyOpt.methods.BayesianOptimization(f=run_bayes, domain=bounds)
my_opt.run_optimization(max_iter=10)

　最適化するには最適化関数(ここでは、run_bayes)を定義します。最適化関数の中ではシミュレーションを行い、目的関数の値を返すようにします。ここでは圧力の値を返しています。これをGPyOpt.methods.BayesianOptimizationのfに渡します。それ以外の部分はこれまでと同じです。この為、数値シミュレーションとベイズ最適化を組み合わせることも非常に簡単に行えます。

The following two tabs change content below.

• この記事を書いた人
• 最新の記事

t-tetsuya

メーカーR&D職 研究開発業務にPythonを使用。 Udemy講師およびKindleで電子書籍を出版。 Udemyでは受講生 約15,000名 Pythonの適用範囲： データ分析、画像処理、統計解析、並列計算、流体解析、深層学習

最新記事 by t-tetsuya (全て見る)

• 【GPyOpt】Python x ベイズ最適化の基本をマスターしよう - 2020年12月29日
• Python print関数の基本の使い方 - 2020年12月10日
• Python関数の書き方の基本 - 2020年12月1日